One of the topics that interest me in C++ is compile-time computation. In this article, we will look at how compile-time computation is done in C++. Compile-time computation can be done in three ways I know of. One is using macros to compute constants, the second way is using template metaprogramming and the other way is using the keyword constexpr to define computations. Since macros are so commonly used, let’s dive into doing compile-time computation using template meta-programming. Let us start with the simplest computation, which is the addition of two numbers. The template should take two arguments, namely x and y and compute the output. This can be done as shown in the code snippet below:
#include <iostream>
template<int x, int y>
struct sum
{
static const int out = x + y;
};
int main()
{
std::cout<<"Sum of 3 and 5 = "<< sum<3,5>::out<<std::endl;
return 0;
}
If you want to ensure that the compiler does the job for you, you can look at the assembly output of the compiler through compiler explorer (gcc 9.1 -O3). The result of the computation is on line 6 which is generated by the compiler. Please note that most of the other generated assembly is for printing the string on to the standard output.
main:
sub rsp, 8
mov esi, OFFSET FLAT:.LC0
mov edi, OFFSET FLAT:_ZSt4cout
call std::basic_ostream<char, std::char_traits<char> >& std::operator<< <std::char_traits<char> >(std::basic_ostream<char, std::char_traits<char> >&, char const*)
mov esi, 8
mov rdi, rax
call std::basic_ostream<char, std::char_traits<char> >::operator<<(int)
mov rdi, rax
call std::basic_ostream<char, std::char_traits<char> >& std::endl<char, std::char_traits<char> >(std::basic_ostream<char, std::char_traits<char> >&)
xor eax, eax
add rsp, 8
ret
Now, let us write such a function for a little-bit more compute-intensive operation, say factorial. A factorial of a number n can be written recursively as \(n imes factorial(n-1)\) . Going recursively inside a function, you eventually reach a point where the factorial(1) needs to be returned. So, for this, a specialization for a value 1 needs to be explicitly mentioned for the compiler to calculate the recursive factorial. See the implementation of the factorial function below.
#include <iostream>
template<int n>
struct factorial
{
static const int out = n * factorial<n-1>::out;
};
template<>
struct factorial<1>
{
static const int out = 1;
};
int main()
{
std::cout<<"Factorial(5)= "<< factorial<5>::out<<std::endl;
return 0;
}
You can also verify this with compiler explorer and check if the generated assembly has the value of \(5!=120\) without explicitly calling any function. Let us do an even more special operation, say \(a^x\).
#include <iostream>
template<int x, int a>
struct power
{
static const int out = x * power<x, a-1>::out;
};
template<int x>
struct power<x, 0>
{
static const int out = 1;
};
int main()
{
std::cout<<"5 ^ 3 = "<< power<5, 3>::out<<std::endl;
return 0;
}
However, using templates for compile-time computation has its own limits. Another interesting function, which I would like to be evaluated is the square root of a number. However, templated arguments can be non-type if it is an integer constant or a pointer to an object with external linkage.
And since square root of any number would evaluate to a float/double, we cannot use templates for such computation. This is one of the situations where I would go for constexpr to evaluate expressions. The square root of a number can be computed recursively using the newton raphson method. There are two implementations below, one in which we compute the square root of a number, in run time(without the use of constexpr) and one in compile-time. This is a very quick and dirty implementation using Newton Raphson, just to illustrate the usage of constexpr. There are more efficient and safe ways to compute the square root of a number.
#include<iostream>
constexpr double EPSILON = 1E-12;
/*computes sqrt during run time, not the most of efficient implementation of
sqrt*/
double sqrt_runtime(double x, double guess = 1)
{
double x_approx = 0.5 * (guess + x/guess);
if((x_approx*x_approx) - x < EPSILON) return x_approx;
else return sqrt_runtime(x, x_approx) ;
}
/*computes sqrt during compile time*/
constexpr double sqrt_compile_time(double x, double guess = 1)
{
return (0.25 * (guess + x/guess) * (guess + x/guess) - x < EPSILON)?(0.5 * (guess + x/guess)):
sqrt_compile_time(x, 0.5 * (guess + x/guess));
}
int main()
{
const double rt_val = sqrt_runtime(200);
std::cout<<"Computed during runtime: "<<rt_val<<std::endl;
constexpr double compile_val = sqrt_compile_time(200);
std::cout<<"Computed during compile time: "<<compile_val<<std::endl;
}
Now, let us benchmark this code quickly using quick-bench. This is a tool which can be used to quickly benchmark your C++ implementations. This is not a very comprehensive benchmark and uses only a single number. This is just to give the reader a idea of how much difference compile time computation can make. The snippet below was benchmarked on quick-bench with the gcc 8.2 (C++11 -O3)compiler. I also included the standard library implementation to the benchmark to check how it compares against our implementation.
#include<iostream>
#include<cmath>
constexpr double EPSILON = 1E-12;
double sqrt_runtime(double x, double guess = 1)
{
double x_approx = 0.5 * (guess + x/guess);
if((x_approx*x_approx) - x < EPSILON) return x_approx;
else return sqrt_runtime(x, x_approx) ;
}
/*computes sqrt during compile time*/
constexpr double sqrt_compile_time(double x, double guess = 1)
{
return (0.25 * (guess + x/guess) * (guess + x/guess) - x < EPSILON)?(0.5 * (guess + x/guess)):
sqrt_compile_time(x, 0.5 * (guess + x/guess));
}
static void RuntimeComputation(benchmark::State& state) {
// Code inside this loop is measured repeatedly
for (auto _ : state) {
constexpr double x = 1000;
double root = sqrt_runtime(x);
}
}
// Register the function as a benchmark
BENCHMARK(RuntimeComputation);
static void CompileTimeComputation(benchmark::State& state) {
// Code before the loop is not measured
for (auto _ : state) {
constexpr double x = 1000;
constexpr double root = sqrt_compile_time(x);
}
}
BENCHMARK(CompileTimeComputation);
static void CPlusPlusStdLib(benchmark::State& state) {
// Code before the loop is not measured
for (auto _ : state) {
constexpr double x = 1000;
constexpr double root = std::sqrt(x);
}
}
BENCHMARK(CPlusPlusStdLib);
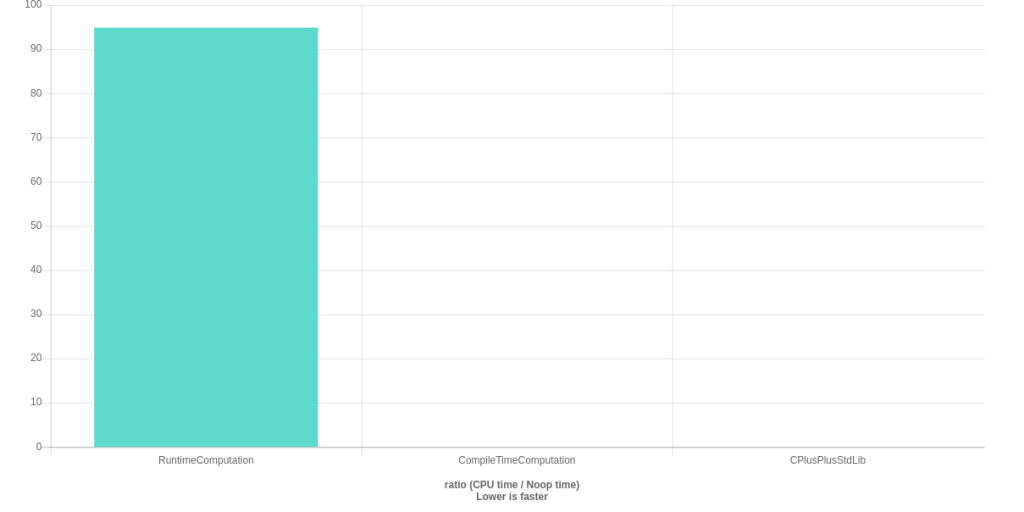
Looking at the results of the benchmark, we can see that compile time computation based implementation is much faster than the run-time computation(~27,000 times faster). It is also interesting to note that our implementation has equivalent performance to the C++ standard library implementation. It would be interesting to see how the C++ standard implements square root, but that discussion is for another day. In summary, use the C++ compiler to do the computations, if you know the value to be computed in advance, either using templates or constexpr.
Thanks for the reading. If you have any questions, please post a comment below.
Some readings on the topic:
https://binary-studio.com/2015/09/18/calculation-at-compile-time-by-help-of-constant-expression/